Fonction cube - Résolution graphique d'équation

Propriété

On se place dans un repère du plan.
On considère la fonction cube \(f\) définie sur \(\mathbb{R}\) par \(x\mapsto x^3\) et \(C_f\) sa courbe représentative dans ce repère.
Les solutions de l'équation \(f(x)=k\) sont les abscisses des éventuels points d'intersection de la droite d'équation \(y=k\) et de la courbe \(C_f\).

Méthode

• Repérer le nombre \(k\) sur l'axe des ordonnées.
  
• Tracer la droite \(\Delta\) d'équation \(y=k\). Cette droite passe par le point de coordonnées \((0~;~k)\) et est parallèle à l'axe des abscisses.
  
• Si \(\Delta\) coupe la courbe \(C_f\), alors les solutions de l'équation \(f(x)=k\) sont les abscisses des points d'intersection de \(\Delta\) et de \(C_f\).
  
• Si \(\Delta\) ne coupe pas la courbe \(C_f\), alors l'équation \(f(x)=k\) n'a pas de solution.
  

Exemple

On se place dans un repère du plan. Soit \(C_f\) la courbe représentative de la fonction cube \(f\) dans ce repère.
Soit `k` un réel de l'intervalle \([-7~;~7]\).
On veut résoudre graphiquement l'équation `f(x)=k`.
Les solutions de cette équation sont les abscisses des points d'intersection de la droite `\Delta` et de la courbe `C_f`.
On les lit sur l'axe des abscisses.

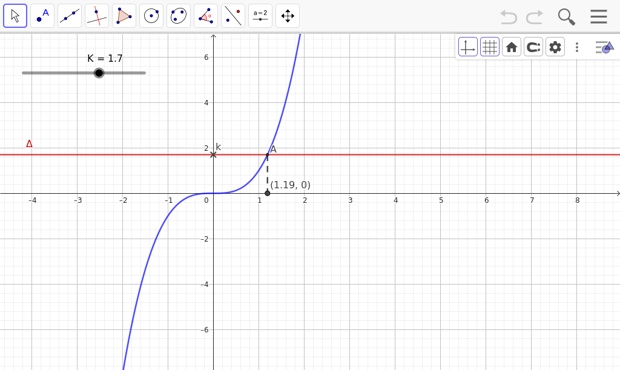
Pour visualiser l'animation, bouger le curseur pour changer la valeur de `k` .

Par exemple :

• pour \(k=1,7\), l'équation \(x^3=k\) admet une solution qui est \(x\approx1,19\) ;
  
• pour \(k=-3,9\), l'équation \(x^3=k\) admet une solution qui est \(x\approx1,57\).